NEURON's reaction-diffusion infrastructure can be used to readily allow intracellular concentrations to respond to currents generated in MOD files, as long as:
- nrn_region='i' is specified for the rxd.Region (so that it knows it corresponds to the electrophysiology region of the inside of the cell), AND
- the name and charge of the ion/etc are given in the rxd.Species declaration.
Satisfying the above two rules also allows MOD files to see intracellular concentrations.
3D extracellular concentrations also interoperate with electrophysiology automatically as long as name and charge are specified.
As a simple example, consider a model with just a single point soma, of length and diameter 10 microns, with Hodgkin-Huxley kinetics, and dynamic sodium (declared using rxd but without any additional kinetics):
# libraries
import matplotlib.pyplot as plt
from neuron import h, rxd
h.load_file('stdrun.hoc')
# define morphology
soma = h.Section(name='soma')
soma.L = soma.diam = 10
# add ion channels (hh is built in, so always available)
soma.insert('hh')
# define cytosol. MUST specify nrn_region for concentrations to update
cyt = rxd.Region([soma], name='cyt', nrn_region='i')
# define sodium. MUST specify name and charge for concentrations to update
na = rxd.Species(cyt, name='na', charge=1)
# record a bunch of variables (this syntax requires NEURON 7.7+)
t = h.Vector().record(h._ref_t)
v = h.Vector().record(soma(0.5)._ref_v)
na_vec = h.Vector().record(soma(0.5)._ref_nai)
ina = h.Vector().record(soma(0.5)._ref_ina)
# current clamp stimuli
ics = [h.IClamp(soma(0.5)) for _ in range(2)]
for i, iclamp in enumerate(ics):
iclamp.amp = 0.3
iclamp.dur = 0.1
iclamp.delay = 5 + i * 15
# initialize and run the simulation
h.finitialize(-65)
h.continuerun(50)
# plot everything
plot_vars = [(v, 'v (mV)'), (ina, 'ina mA/cm$^2$'), (na_vec, '[Na$^+$] (mM)')]
for i, (vec, name) in enumerate(plot_vars):
plt.subplot(len(plot_vars), 1, i + 1)
plt.plot(t, vec)
plt.ylabel(name)
plt.show()
Our test cell gets two brief current stimuli, which cause it to fire. With each action potential, a small amount of sodium enters the cell, raising the cell's intracellular sodium concentration.
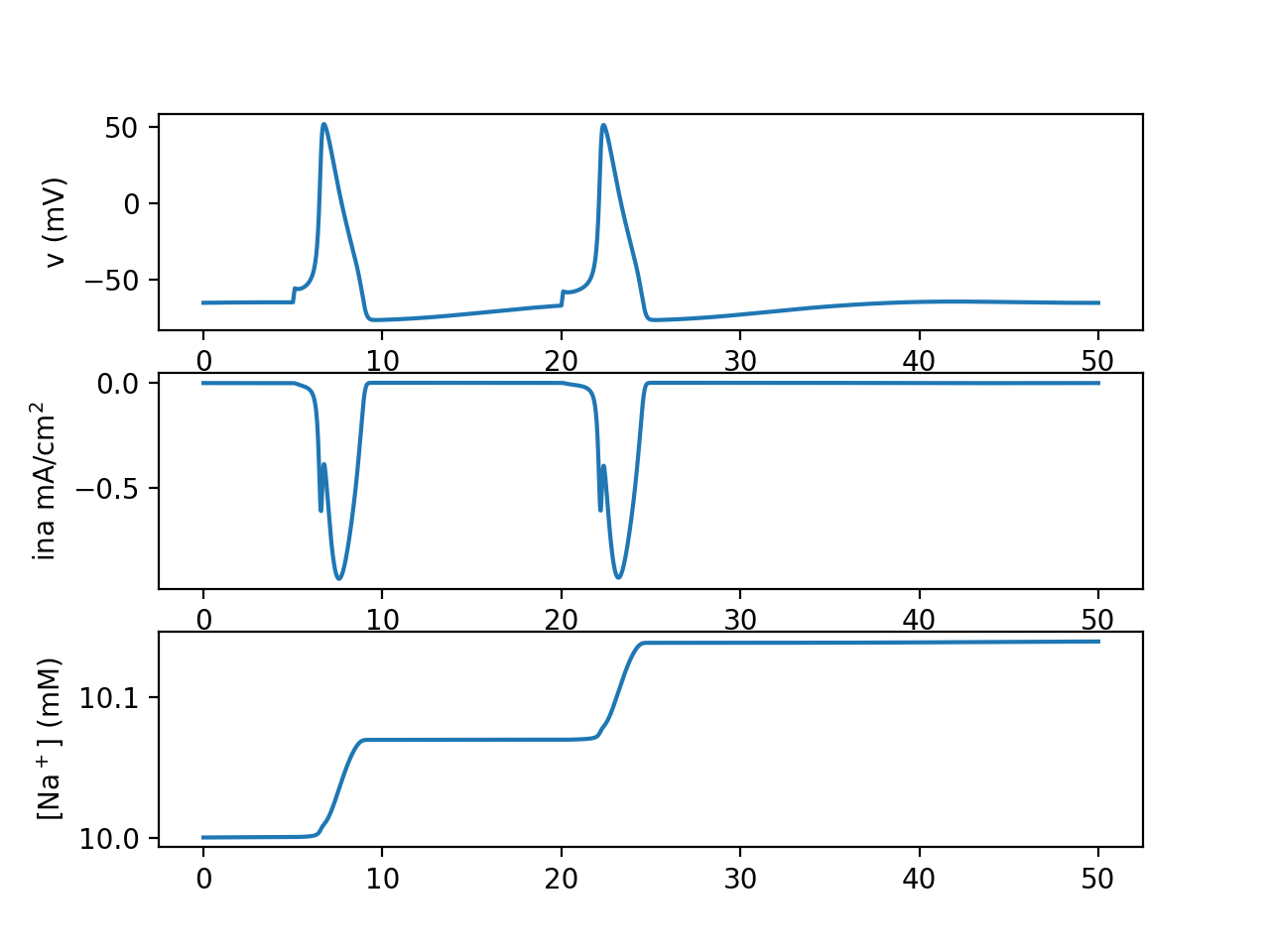
Without any additional homeostatic mechanisms (Hodgkin and Huxley did not model sodium concentration so they did not need to include homeostatic mechanisms for it), intracellular sodium concentration will not return to baseline, and each spike will move intracellular sodium concentration closer to the extracellular concentration. Potassium concentration in this model is constant as we did not declare a potassium rxd.Species, but if we did it would also approach its extracellular concentration with each spike, until eventually the cell is not able to fire action potentials anymore.