Hi, first post. I've been digging into potassium channel kinetics, specifically trying to match Choi and Waxman 2011. It SHOULD be rather straightforward. For example, the gating given for K-A channel is n*h and the authors give an equation for steady-state "n" of:
Eq 1. ninf = (1/(1+exp(-(V+5.4)/16.4)))^4
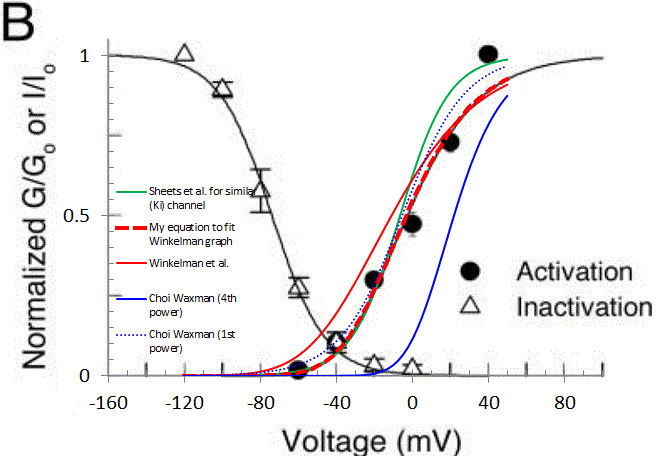
This equation was cited as being derived from Sheets, et al. 2007, and is identical to the original. But this equation, with parameters given (blue trace in graph below), ends up giving an effective Vhalf of about +22mV which I believe is not physiological. For example, Winkelman et al. 2005 show a graph with Vhalf of about -42mV for K-A channels (solid black trace on original plot), and this seems consistent with other sources.
Moreover, implementing all the K-A channel equations (for tau n, hinf, and tau h) as cited in Choi Waxman, and calculating I_KA = gKA * n * h * (V-EK) and running a step protocol (-120mV up to various terminal voltages) gives currents that do not agree with those cited in the paper. Now, I'm also implementing my model in another environment (JDesigner, part of the Systems Biology Workbench), and so it's possible that the equation form given is not what the authors actually implemented in NEURON. If they set up their model to accept APPARENT Vhalf (=-5.4mV) and k (inverse slope, here = 16.4), and calculated the corresponding parametes, they'd get a parameterization similar to:
Eq. 2 ninf = (1/(1+exp((V-(-42.0))/-23.25)))^4
This is the bold red dashed line in the plot below. This last equation matches a graph (and the datapoints) in Winkelman et al. But Winkelman et al. give an equation of
Eq. 3 ninf = (1/(1+exp((V-(-60.3))/-29.6)))^4
(solid red line in plot) for the same data, and this last function definitely doesn't match their data.
Here is a plot from Winkelman et al. I've overlayed a graph and plotted data from another paper by Sheets et al., to show that we have a somewhat consistent picture of K-A gating. The other curves have been described, except that the 4th order function cited by Choi Waxman, and derived from Sheets et al. (solid blue curve) and it doesn't match the Winkelman or Sheets data very well. But if you plot that same function to the 1st order (dotted blue line), it DOES match resonably well.
So, am I going crazy here? Is there a secret decoder ring (or a model file that folks use) that implements the Boltzmann 4th Power function in which parameters are adjusted? Why are equations given by several authors not matching simulation results given in the source (Choi Waxman), or the fitted function plotted in the source (Winkelman)? Or did I just happen to be unlucky in which equations I grabbed? Many thanks.
1. Choi J-S, Waxman SG. Physiological interactions between Nav1. 7 and Nav1. 8 sodium channels: a computer simulation study. J Neurophysiol. 2011;106(6):3173–3184.
2. Sheets PL, Jackson JO, Waxman SG, Dib-Hajj SD, Cummins TR. A Nav1. 7 channel mutation associated with hereditary erythromelalgia contributes to neuronal hyperexcitability and displays reduced lidocaine sensitivity. J Physiol. 2007;581(3):1019–1031.
3. D. L. B. Winkelman, C. L. Beck, D. L. Ypey, and M. E. O’Leary, Inhibition of the A-Type K Channels of Dorsal Root Ganglion
Neurons by the Long-Duration Anesthetic Butamben, J. Pharma & Exp. Therapeutics, 2005, 314(3):1177-1186