The Electrotonic Workbench

N.T. Carnevale1,2
K.Y. Tsai3
and M.L. Hines1,4

1Neuroengineering and Neuroscience Center
and Departments of 2Psychology and 4Computer Science
Yale University, New Haven, CT,
and 3Harvard Medical School
Boston, MA

Abstract

We present the Electrotonic Workbench, a new set of software tools for analyzing the electrotonic architecture of neurons. These tools, which were created using the simulation program NEURON [Hines 1989, 1993], implement the empirically-based analytical strategies that we and our collaborators have described elsewhere [Brown et al. 1992; Carnevale et al. 1995a; Tsai et al. 1994; Zador et al. 1995] and have used to study electrical signaling in neurons [Carnevale et al. 1995b]. They run on all platforms to which the fully graphical version of NEURON has been ported (workstations and PCs under the Xwindows or MS-Windows 3.1, NT, and 95 environments). Unlike some tools that have been used for similar purposes [Zador et al. 1995], they do not require the purchase of commercial software. Therefore the Electrotonic Workbench is maximally accessible to experimentalists and theoreticians who need a practical and convenient way to examine the functional consequences of neuronal anatomy and biophysics.

The Electrotonic Workbench operates in the following manner.
1. The anatomy and biophysical properties of the cell are specified by the user through any of the usual data entry mechanisms (i.e. read from files, created algorithmically, entered or edited manually, or any combination thereof).
2. Since attenuation depends on direction of signal propagation [Tsai et al. 1994], NEURON computes the voltage attenuations along each branch of the model for signals propagating away from (Vout) and toward (Vin) a user-selected reference point. The reference point, which can be any functionally or anatomically relevant location in the cell, may be selected via NEURON's graphical interface. Attenuation is a function of frequency, so it is often informative to compute a pair of Vout and Vin transforms at several frequencies of interest. Because voltage attenuation in one direction is the same as current or charge attenuation in the opposite direction, the Vout and Vin transform pairs provide a complete picture of the electrotonic architecture of the cell.
3. Graphical renderings of the Vout and Vin transforms are generated, in either the "neuromorphic" or "L vs. x" [O'Boyle et al. 1996] format. The neuromorphic renderings, which we demonstrate in this abstract, give the quickest intuition to the electrotonic architecture of a neuron. These redraw the cell in a way that preserves its overall shape, but with the distances between adjacent measurement points proportional to the logarithm of voltage attenuation between them. Since attenuation depends on direction of signal propagation [Tsai et al. 1994], each anatomical branch has two representations in electrotonic space depending on which of its ends is "upstream" from the other. The proximal ends are "upstream" in the Vout transforms (centrifugal propagation of voltage), whereas the distal ends are "upstream" in the Vin transforms (centripetal propagation of voltage).
4. Numeric results are available for subsequent quantitative analysis and can be written to output files as appropriate.

Computations and graphical renderings are all handled in an integrated fashion because the Electrotonic Workbench runs within the NEURON environment. This means the user can examine the results immediately and is not bothered with details such as moving intermediate data files between different programs. Furthermore, all operations are customizable and under program control, so the user can automate a series of analyses that iterate over a range of frequencies, biophysical parameters, anatomical dimensions, or combinations thereof.

Methods

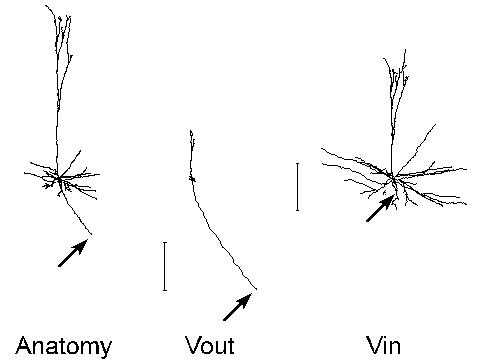
For the purpose of illustration, we show the transforms of the neocortical pyramidal cell whose morphometric data accompanies the standard NEURON distribution (($NEURONHOME)/nrn/demo/pyramid.nrn). The biophysical parameters we used are Ra = 200 ohm-cm, Rm = 14,500 ohm-cm^2, Cm = 1 uf / cm^2, with a uniform spine density that adds 1.25 um^2 per um length of neurite [Cauller and Connors 1992]. The transforms and their graphical renderings were performed with NEURON executing the Electrotonic Workbench under MS-Windows 3.1 on a 90 mHz Pentium PC with 16 MB RAM. Computation and display of the Vout or Vin transform was complete within 1 second for this model cell with 79 segments. All images were captured directly from the VGA display using HiJaak Pro, and subsequently composed and labeled with HiJaak Draw (HiJaak Graphics Suite v. 3.0, Inset Systems, Inc.).

Observations described below are similar to findings that we have reported elsewhere in hippocampal pyramidal neurons [Carnevale et al., 1995b].

Results

Electrotonic architecture at 0 Hz: somatic reference

On the left is a side view of the anatomy of the cell. The center and right images are the neuromorphic renderings of the Vout and Vin transforms relative to the soma at 0 Hz. The calibration bars are in "log attenuation" units (one unit of separation in electrotonic space corresponds to an e-fold decay of voltage). Because the soma is the "reference point" for the transforms shown in this and the following figure, electrotonic distance is to be measured away from the soma in the Vout image, and toward it in the Vin image.

Note that:

Electrotonic architecture at 40 Hz: somatic reference

Attenuation increases rapidly with frequency, as these transforms demonstrate. Consequently, at 40 Hz the spatial scope of action for signals generated in the soma or dendrites would be very limited (i.e. localized processing predominates). Based on this electrotonic architecture, one would expect that synaptic inputs responsible for network synchronization at high frequency should be located quite near the soma. Modeling studies [Lytton and Sejnowski 1991] and experimental observations [Ylinen et al. 1995] support this prediction in hippocampus.

Electrotonic architecture at 0 Hz: dendritic reference

A somatic reference point is the most logical choice when one is concerned with issues such as

However, a nonsomatic reference is preferable for other purposes, such as studying associative interactions among different synaptic inputs. We have pointed out that the only difference between the transforms for a somatic reference and a nonsomatic reference D is along the direct path between the soma and D, where the direction of signal propagation changes [Tsai et al. 1994]. Along this path the Vout transform relative to D is the same as the Vin transform relative to the soma; in all the other neurites, signal propagation is away from both D and from the soma, so attenuations are unchanged.

This is clearly seen by comparing the central image (Vout) of the following figure (dendritic reference location D indicated by arrow) with the Vout and Vin transforms in the first figure (Electrotonic architecture at 0 Hz: somatic reference).

Likewise, along this path the Vin transform relative to D is the same as the Vout transform relative to the soma, but elsewhere the Vin transforms are identical (compare right image of this figure with the Vout and Vin transforms in the first figure (Electrotonic architecture at 0 Hz: somatic reference).

Since the "reference point" for the transforms shown in this figure is dendritic location D (arrow), electrotonic distance is to be measured away from D in the Vout image, and toward D in the Vin image. For the sake of clarity, D was placed on a termination, but any other nonsomatic location could have been used.

Bibliography

  1. Brown, T.H., Zador, A.M., Mainen, Z.F., and Claiborne, B.J.. Hebbian computations in hippocampal dendrites and spines. In: Single Neuron Computation, ed. McKenna, T., Davis, J. and Zornetzer, S.F.. New York: Academic Press, 1992, pp. 81-116.
  2. Carnevale, N.T., Tsai, K.Y., Claiborne, B.J. and Brown, T.H.. The electrotonic transformation: a tool for relating neuronal form to function. In: Advances in Neural Information Processing Systems 7, eds. Tesauro, G., Touretzky, D.S., and Leen, T.K.. MIT Press, Cambridge, MA, 1995a, pp. 69-76.
  3. Carnevale, N.T., Tsai, K.Y., Claiborne, B.J. and Brown, T.H.. Qualitative electrotonic comparison of three classes of hippocampal neurons in the rat. In: The Neurobiology of Computation: Proceedings of the Annual Computational Neuroscience Meeting 1994, ed. Bower, J.M.. Kluwer, Boston, MA, 1995b, pp. 67-72.
  4. Cauller, L.J. and Connors, B.W.. Functions of very distal dendrites: experimental and computational studies of layer I synapses on neocortical pyramidal cells. In: Single Neuron Computation, ed. McKenna, T., Davis, J. and Zornetzer, S.F.. New York: Academic Press, 1992, pp. 199-229.
  5. Hines, M.. A program for simulation of nerve equations with branching geometries. Int. J. Biomed. Comput. 24:55-68, 1989.
  6. Hines, M.. NEURON -- A program for simulation of nerve equations. In: Neural Systems: Analysis and Modeling, ed. Eeckman, F.. Norwell, MA: Kluwer, 1993, p. 127-136.
  7. Lytton, W.W. and Sejnowski, T.J.. Simulations of cortical pyramidal neurons synchronized by inhibitory interneurons. J. Neurophysiol. 66:1059-1079, 1991.
  8. O'Boyle, M.P., Carnevale, N.T., Claiborne, B.J., and Brown, T.H.. A new graphical approach for visualizing the relationship between anatomical and electrotonic structure. In: Computational Neuroscience: Trends in Research 1995, ed. Bower, J.M., San Diego, CA: Academic Press, 1996, p. 423-428.
  9. Tsai, K.Y., Carnevale, N.T., Claiborne, B.J., and Brown, T.H.. Efficient mapping from neuroanatomical to electrotonic space. Network 5:21-46, 1994.
  10. Ylinen, A., Bragin, A., Nadasdy, Z., Jando, G., Szabo, I., Sik, A. and Buzsaki, G.. Sharp wave-associated high-frequency oscillation (200 Hz) in the intact hippocampus: network and intracellular mechanisms. J. Neurosci. 15:30-46, 1995.
  11. Zador, A.M., Agmon-Snir, H., and Segev, I.. The morphoelectrotonic transform: a graphical approach to dendritic function. J. Neurosci. 15:1669-82, 1995. These authors used Mathematica to compute transforms. They have posted the toolkit they developed.

Address correspondence to:
N.T. Carnevale
Psychology Dept.
Yale University
P.O. Box 208205
New Haven, CT 06520-8205
phone 203-432-7363
fax 203-432-7172
email ted.carnevale@yale.edu

Page and images Copyright © 1996, 1999 N.T. Carnevale. All RightsReserved.