A. Parameter specification
The function is
A*(exp(-k1*$1) - exp(-k2*$1))and its parameters are A, k1, and k2. We want the optimizer to be able to adjust all of these in order to fit the function to the data.
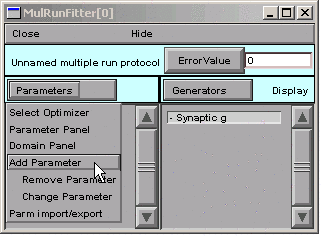
In the MRF, clicking on Parameters / Add Parameter

brings up a tool for specifying the name of a parameter.
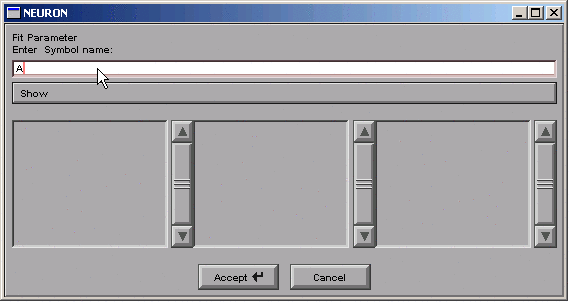
We click in edit field, type A, and then click on the Accept button.
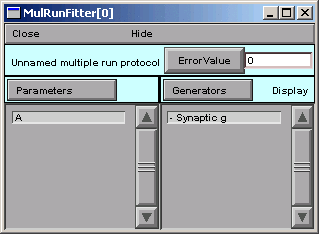
The left panel of the MRF now contains "A".
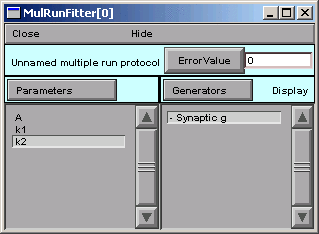
We repeat the same sequence for k1 and k2.
The MRF finally looks like this,
with A, k1, and k2 appearing in its left panel.
Save to a session file!
B. Testing the Generator
Let's see if things are working properly.
In the Generator, we click on the Error Value button.
This makes the Generator evaluate and plot the function.
The Generator also computes the sum of squared error between the
function and the experimental data for every value of the independent variable
in the interval bracketed by the blue lines.

The Error Value field shows a nonzero value, suggesting that the Generator is working OK.
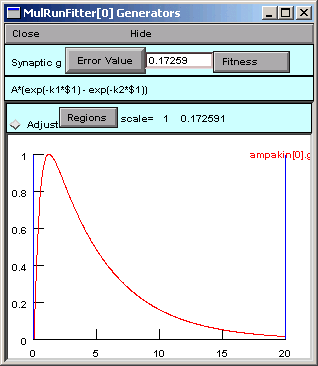
But where is the black trace that shows the trajectory of the parameterized function?
Ah, we completely forgot about the values of the parameters.
C. Viewing (and changing) parameter values
In the MRF, we click on Parameters / Parameter Panel
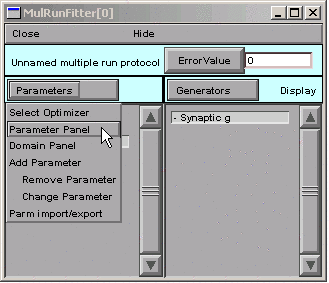
A = 1 (good), but k1 = k2 = 1, so our function is 1 times the difference between two identical exponentials, i.e. 0.

In the Generator you can click on the the x axis and confirm that a trace is there (crosshairs will appear, and you can run the crosshairs along the length of the x axis).
Let's change a parameter so we can see this trace.
In the Parameter panel, we change k2 to 10.
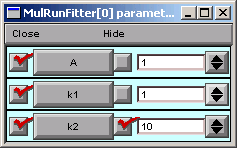
Now we go back to the Generator and click on Error Value again.
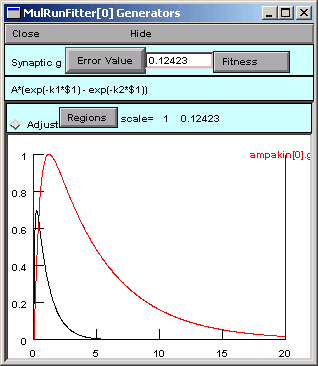
A small black curve appears--we're on the right track.
You don't absolutely have to save a session file now, but what harm could it do?
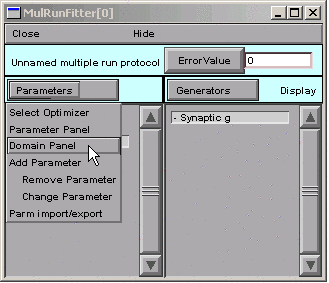
D. Constraining parameters
Now it's time to consider the topic of constraining parameters, first from the perspective of this particular problem, and then in more general terms.
In the MRF, we click on Parameters / Domain Panel
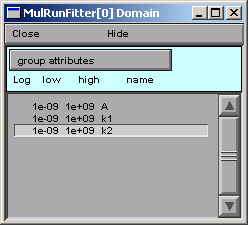
This brings up the MulRunFitter Domain panel,
which shows that all parameters are unbounded,
i.e. they are free to vary from -1e9 to 1e9.
Given the apperance of the data and the form of our function
we can tell that
the objective function will have two minima:
one with A > 0 and k1 > k2 > 0,
and the other with A < 0 and k2 > k1 > 0.
Let's say we want to find the one with A > 0.
So in the MulRunFitter Domain panel we click on
group attributes / positive definite limits

Now the parameters are constrained to lie between 1e-9 and 1e9.
It's OK to close the MulRunFitter Domain panel; we can always bring it up again if we need it.
Restricting parameter space
For some optimization methods, e.g. random search algorithms, convergence can be improved by "fencing off" parts of parameter space that we aren't interested in. However, the PRAXIS optimizer used by NEURON requires a continuous objective function, so restricting parameter space can actually interfere with it. Nevertheless, it is always a good idea to at least restrict the parameter space to those regions where the objective function does not crash, since you never know what path an optimizer will take to reach its goal. For example, negative capacitance or conductance will generally make a simulation unstable, and 0 or negative concentrations will give a math error when the Nernst equation is calculated.
Log scaling
PRAXIS often benefits from logarithmic scaling of parameters. Our experience suggests that this is most helpful when two or more parameters are very different in size, e.g. when they differ by orders of magnitude. To take advantage of log scaling, make sure that the problem is stated in a way that allows you to set a group attribute of "positive definite limits", and then set the "use log scale" group attribute. The performance improvement over linear scaling can be quite striking.
We have already stipulated that the parameters be positive definite, so we might as well go ahead and use log scaling. Later on we'll try linear scaling and compare the results.
Range constraints and log vs. linear scaling can also be set for individual parameters. This is discussed in the help files (look in the alphabetical listing for MulRunFitter).
Save to a session file before proceeding any further!
Copyright © 2004 by N.T. Carnevale and M.L. Hines, All Rights Reserved.