Specify channel gating: voltage and ligand dependence

Step 3. Specify channel gating continued

C. Specify the equations that describe the voltage sensitivity of state transitions.

First make sure that the Properties radio button is ON.

The C1-C2 transition

Click on the C1-C2 transition and notice what happens to the GateGUI.

The panel to the right of the canvas contains controls for specifying the "Power" for O and the "fractional conductances" of the closed states C1 and C2. For this mechanism, these parameters should be 1, 0, and 0, respectively.

"Power" is useful for mechanisms in which the conductance depends on cooperative interactions among "open" states.

Example: if conductance requires interactions between pairs of O states, the Power should be 2 and the total conductance will be
g = gmax * O^2

"Fractional conductance" is useful for kinetic scheme mechanisms that have more than one conductive state. The total conductance is proportional to the weighted sum of all conductive states.

Example: if the single channel conductance associated the C1 and C2 states were 0.1 and 1.5 times that of the O state, we would set the "C1 fraction" to 0.1 and the "C2 fraction" to 1.5. The total conductance would then be
g = gmax * (O + 0.1*C1 + 1.5*C2)

Now we need to specify the voltage dependence of the C1 - C2 transition. By default the EquationType uses the alpha,beta style. We already have the equations for a1 and b1

        a1 = K1/(tau1*(K1+1))
        b1 =  1/(tau1*(K1+1))

so this looks like a piece of cake. Just substitute

        tau1 = ta1*exp(tk1*vr)
        K1 = exp((k2*(d2 - vr)) - (k1*(d1 - vr)))

and rearrange, and we get

        a1 = ta1*exp(-tk1*vr)/(1 + exp(k1*(d1-vr) - k2*(d2-vr))

So we look in the menu of alpha,beta functional forms

and find nothing. The expression for a1 just doesn't simplify to anything in this list. We're cooked.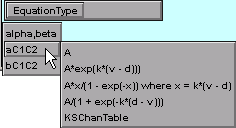

Or are we?

Recalling that

        tau = 1/(a+b) and inf = a*tau

we realize that the tau,inf formulation yields functional forms that are amenable to the Channel Builder. For tau we get

        tau = 1/(a+b) = tau1*(K1+1) / (1+K1) = tau1 = ta1*exp(tk1*vr)
            = ta1*exp(tk1*(v+65))
            = 4.4*exp(-0.025*(v+65))

which is the exponential functional form with A = 4.4, k = -0.025, and d = -65.

Turning to inf,

        inf = a*tau = a1*tau1 = K1/(K1+1)
        1/inf = 1 + exp(-k2*(d2 - vr) + k1*(d1 - vr))

Focussing on the exponent,

        -k2*(d2 - vr) + k1*(d1 - vr) = k1*d1 - k2*d2 - (k1-k2)*vr
          = (k1-k2)*( ((k1*d1 - k2*d2)/(k1-k2)) - 65 - v )
          = 0.164*( (4.2 - 1.548)/0.164 - 65 - v )
          = 0.164*(2.652/0.164 - 65 - v)
          = 0.164*(16.2 - 65 - v) = 0.164*(-48.8 - v)

        inf = 1/( 1 + exp(0.164*(-48.8 - v)) )

which is the logistic functional form with A = 1, k = -0.164, and d = -48.8

So we select the inf,tau type of equations

Also, we might as well click on "Display inf, tau" so we can see how inf and tau vary with membrane potential.

Finally we select the functional forms for inf and tau, and assign the parameter values.

For inf, click on
EquationType / infC1C2 / A/(1 + exp(k*(d-v)))

The equation displayed for infC1C2 will change, and new buttons and numeric fields will appear for setting the values of A, k, and d. Enter the values of these parameters into the corresponding numeric fields (A = 1, k = -0.164, d = -48.8).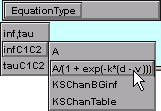

Now for tau. Select the exponential functional form by clicking on
EquationType / tauC1C2 / A*exp(k*(v - d)))

After entering the values for tauC1C2's parameters (A = 4.4, k = -0.025, d = -65), and rescaling the graph in the bottom panel (using View = plot, or better, Set View), the GateGUI tool will look like this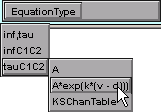

Was there ever a better time to save a session file?

The C2-O transition

Let's deal with the algebra first. For reaction 2 we have

        tau = tau2 = ta2*exp(tk2*vr)
            = ta2*exp(tk2*(v+65))
            = 2.6*exp(-0.007*(v+65))

Like tau for the C1-C2 transition, this is just the exponential form, but with different parameters (A = 2.6, k = -0.007, d = -65).

What about inf? This time we get a little break --

        inf = K2/(K2+1)
            = 1/(1 + exp(k2*(d2 - vr)))
            = 1/(1 + exp(0.036*(43 - 65 - v)))
            = 1/(1 + exp(0.036*(-22 - v)))

which is the logistic form with A = 1, k = -0.036 and d = -22

click on the C2-O transition
select the inf,tau style
click on the "Display inf, tau" checkbox
choose the appropriate forms for infC2O and tauC20,
and
fill in their parameters

After rescaling the graph, the GateGUI should look like this

Just out of curiousity, you might want to examine the voltage dependence of a and b for the C1-C2 and C2-O transitions. But don't expect them to look like the hh rate constants.

Before moving on, save the Channel Builder to a session file!

The next step is to test our new channel in a model cell.

[ Outline | Previous | Next ]